电流做功
电功
电流可以做功。简称电功。
例如:电热水壶把电能转化为热能,电动机把电能转化为机械能。
公式
电流做功的多少跟电流的大小,电压的高低,通电时间的长短都有关系。加在用电器上的电压越高、通过的电流越大、通电时间越长,电流做功越多。电工单位是焦耳(\(J\))。
电功率
电功率就是单位时间内电流做功的多少。
例如小灯泡与一个很大的电阻串联,不发光或者光很微弱,就是因为小灯泡的功率太小。
公式
如果电路是纯电阻电路,即所有的电能都转化为热能(电热水壶、电热毯等),那么由于此时欧姆定律成立,则有以下的公式。
(特殊情况:白炽灯由于是温度升高而发光的,所以也算纯电阻电路,因此以上的公式是适用的。)
对于初中物理考试情况,计算题一般是不会考非纯电阻电路的,所以以上公式都可以用。
在串联电路中,由于电流处处相等,所以 \(P_1:P_2:P_3=U_1:U_2:U_3=R_1:R_2:R_3=W_1:W_2:W_3=Q_1:Q_2:Q_3\)。
在并联电路中,由于支路电压处处相等,所以 \(P_1:P_2:P_3=U_1:U_2:U_3=\cfrac{1}{R_1}:\cfrac{1}{R_2}:\cfrac{1}{R_3}=W_1:W_2:W_3=Q_1:Q_2:Q_3\)。
电功率的变化量
现在有如下的一个电路(电源电压不变)。
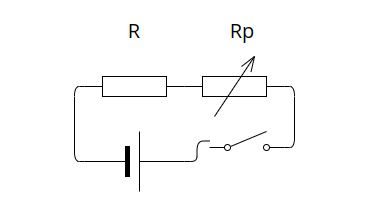
已知电路中的电流变化量为 \(\Delta I\),华东变阻器或定制电阻两端的电压变化量为 \(\Delta U\)(这两者实际上相等,因为两者两端的电压之和等于不变的电源电压)。求电功率的变化量 \(\Delta P\)。
我们列方程可以求解得到 \(R = \cfrac{\Delta U}{\Delta I}\)。那么 \(\Delta P\) 就可以算出来了。
(注意到 \(\Delta P\) 并不等于我们直觉上认为的 \(\Delta U \times \Delta I\)。)
问题来了,有了 \((I_1+I_2)\times\Delta U\) ,那么与之相对应的 \((U_1+U_2)\times\Delta I\) 是不是存在呢?
确实存在。只需要在推导时把第二步中的 \(I_2^2R-I_1^2R\) 换成 \(\cfrac{U_2^2}{R} - \cfrac{U_1^2}{R}\) 即可。
作用:这个公式,在已知 \(\Delta I\) 和 \(\Delta U\) 的时候或许没什么用;但是在已知 \(\Delta P\) 求剩下的量时,是很有用的,因为就不需要列方程了。
电功率的图像问题
问题:还是前文提到的电路,只不过求华东变阻器的功率最大值。
推导如下(顶置电阻为 \(R_1\),华东变阻器为 \(R_2\))。
因为要使得 \(P_2\) 最大,所以分母需要最小,则 \(\cfrac{(R_1-R_2)^2}{R_2}\) 最小。又因为 \((R_1-R_2)^2\) 是非负数,所以当 \(R_1 = R_2\) 时,有最大值 \(\cfrac{U^2}{4R_1}\)。
以下是\(P_2\) 和 \(R_2\) 的图像(注意这不是二次函数)。
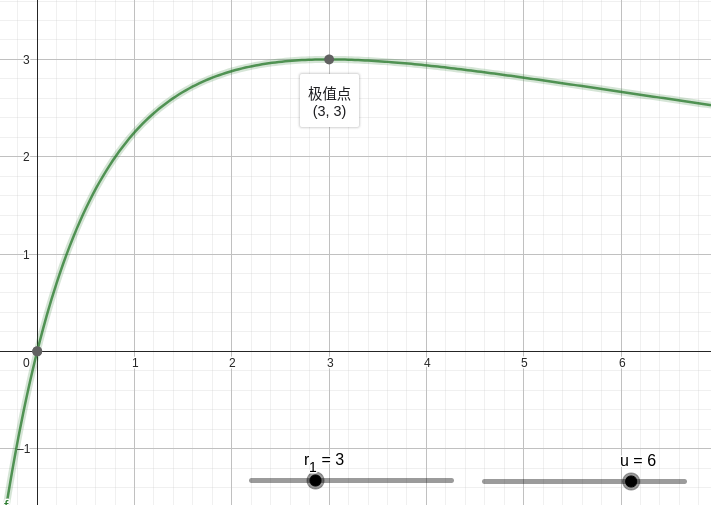
规律:若有 \(P_A = P_B\),且 \(R_A \neq R_B\),则 \(R_AR_B = R_1^2\)。
证明:解方程找 \(R_1,R_2\) 关系即可,如下。