力的分解

引入

我们在教科书上学习了力的合成与分解，但那是同一直线上的。但在生活中的大部分情况下，力并非严格沿着同一直线。因此本文将在这里介绍不同直线上的力是如何合成/分解的（事实上我们将着重介绍分解，因为合成其实就是逆向分解）。

方法

我们来看下面这张图：

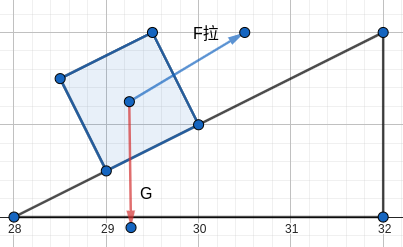
（\(\tan \theta_{斜面} = \frac{1}{2}, G_{物} = 300\sqrt{5} N, F_{拉} = 400 N, f = 100 N\)，并且匀速拉动物体）

我们可以对这个在斜面上的物体进行受力分析，惊奇地发现 \(f \neq F_{拉}\)。这是为什么呢？

读者可以自行思考一下。

其实是因为重力在摩擦力的方向上还有一个分力。那求出这个分力就成了我们的目标。在这里我们自然想到了以\(f\)的方向作一根直线当作\(X\)轴，物体重心当作原点，然后以另一根过原点并与\(X\)轴垂直的直线当作\(Y\)轴，建立一个平面直角坐标系。然后以重力的那条线为斜边，构造一个直角三角形，就像这样：

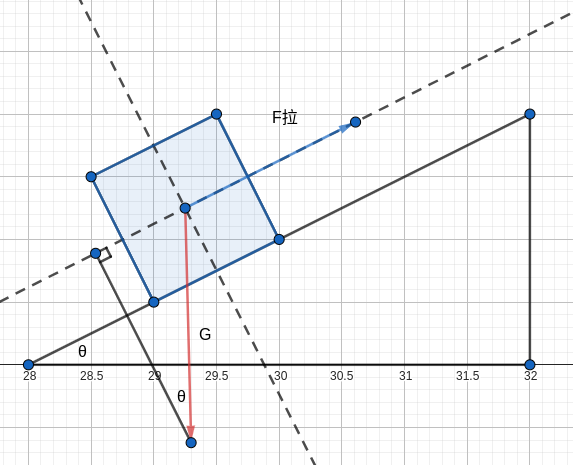
我们计算一下角度，不难发现大直角三角形与小直角三角形是相似的。这样我们只需要运用 \(\tan \theta_{斜面} = \frac{1}{2}\)，计算得出重力在\(X\)轴上的分力为 \(F_{G分} = 300 N\)，正好发现符合平衡条件\(f + F_{G分} = F_{拉}\)。

这样我们就掌握了基本方法。

实战

筷子平衡问题：

（提示：筷子所受的摩擦力方向是向碗的圆心，初中物理没法解释）

如图所示，碗是一个半球形，直径 \(36cm\)，两端口水平，一个筷子（粗细不计，且密度分布均匀），长度为 \(47cm\)，搁置在碗上。碗的厚度不计。在筷子平衡时，碗内部分与碗外部分的长度比是多少？

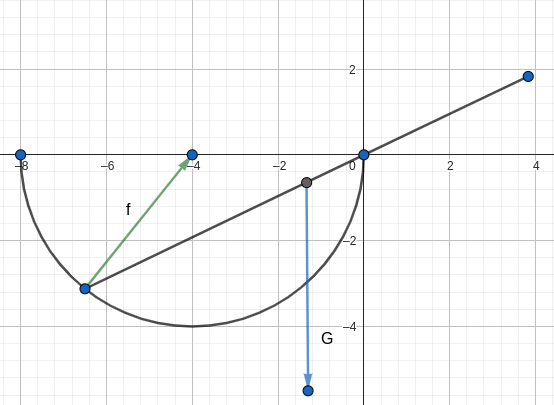
（符号：\(f\) 筷子摩擦力，\(G\) 筷子重力，\(L_1,L_2\) 力臂，\(\sin, \cos, \tan, \cot\) 一些三角函数，\(\theta\) 夹角，\(a\) 筷子碗内长度，\(b\) 筷子碗外长度）

不难发现这根筷子本质是一个杠杆，并且支点为接触点。所以我们可以先把摩擦力的力臂做出来。这样我们就根据杠杆的平衡条件得到了第一个式子： \(f \times L_1 = G \times L_2\)，其中 \(L_1 = a \sin \theta\)，\(L_2 = (\frac{47}{2} - b) \times \cos \theta\)。

然后我们发现仅仅有这一个条件是远远不够的。因为筷子作为一个物体，他需要本身受力平衡。这方面主要是沿着筷子自身方向的力。因此我们就必须把 \(G\) 和 \(f\) 分解出来他们各自在筷子方向上的分力。采用我们之前的方法即可。

如图：

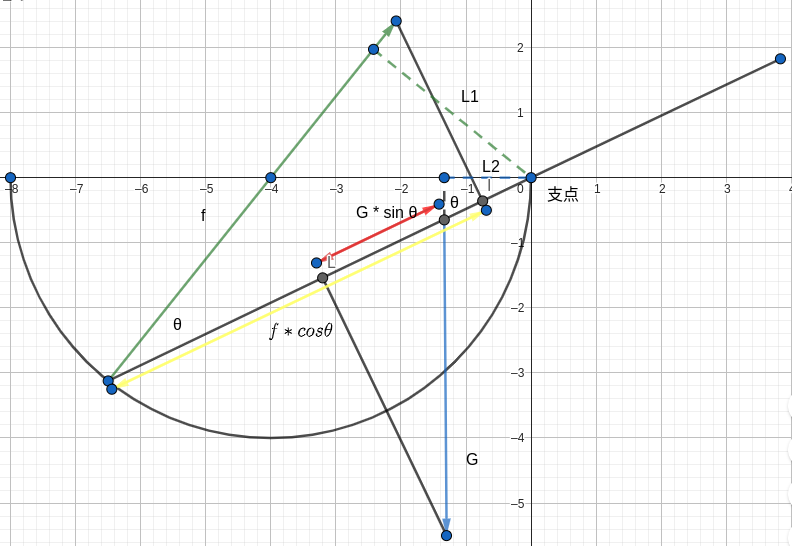
我们经过分析算出筷子方向分力是 \(f \times \cos \theta\) 和 \(G \times \sin \theta\)。

因此我们得到两个方程：

\[ f \times \cos \theta = G \times \sin \theta \]

\[f \times a \sin \theta = (\frac{47}{2} - b) \times G \times \cos \theta\]

我们发现上面跟下面都有相同的 \(f,G\)，所以我们可以两式相除得到\(a\times \tan \theta = (\frac{47}{2} - b) \cot \theta\)，然后继续化简。得到：\(a \times \tan^2 \theta = \frac{47}{2} - b\)。我们稍微计算一下角度就会发现其实 \(\tan \theta = \frac{L_垂}{a}\)，（\(L_垂\) 是接触点到直径左边端点的距离），为何？因为直径所对的圆周角就是直角。由此我们得到了结果：

\[L_垂^2 = a \times (\frac{47}{2} - b)\]

配图方便理解：

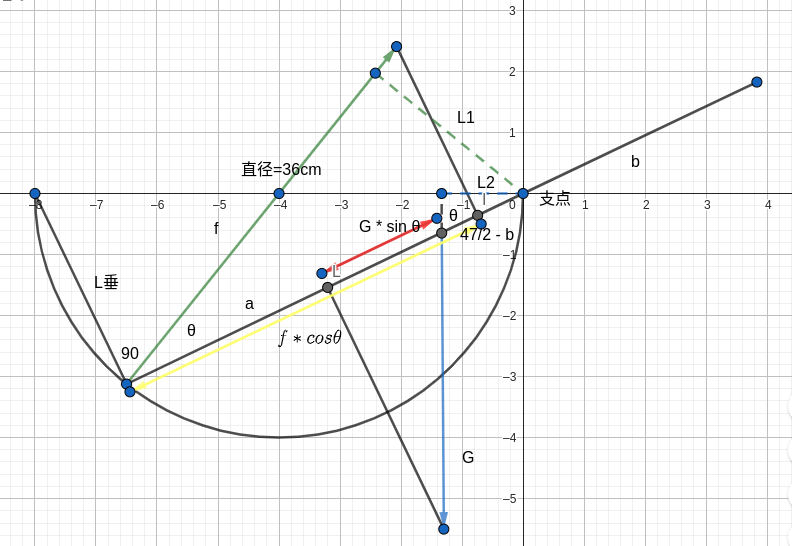
同时我们根据勾股定理得到：

\[L_垂^2 = 36^2 - a^2\]

那么我们在把 \(b\) 替换为 \(47 - a\)，就能得到一个一元二次方程：

\[36^2 - a^2 = a(a - \frac{47}{2})\]

这里你应该会求解了。解出来：

\[a_1 = 32, a_2=-\frac{81}{4}(舍弃)\]

那么最终结果就是 \(32 : 15\)。

评论