快速弹簧算法(FSA)
介绍
这个算法由BsoltB发明,用于解决浮力的弹簧类问题。
FSA第一部分:加水减水
公式推导
先看一张图:
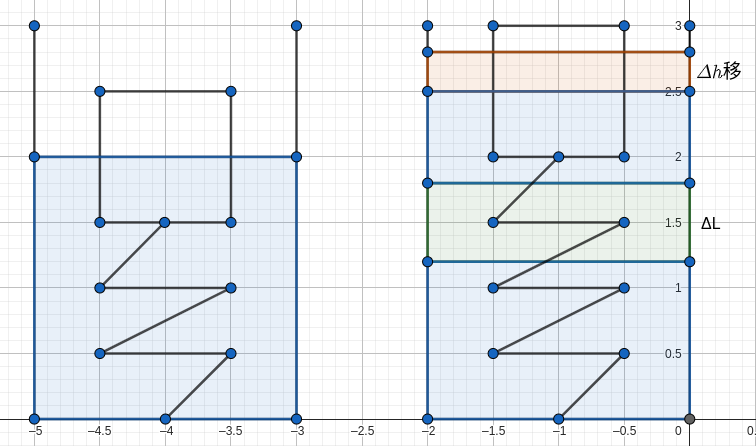
其中蓝色是原来的水,红色+绿色是加的水。这部分水加进去会影响弹簧长度,则有长度变化量\(\Delta L\)。并且物体也会移动,则有移动距离\(\Delta h_{移}\)。
由此我们可以得出第一个式子:
以及第二个式子:
继续看第二张图:
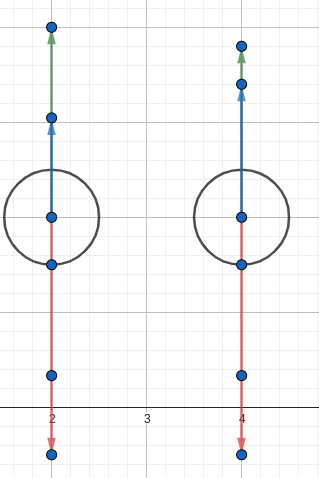
图中我们对物体进行了受力分析,红色是 \(G\),蓝色是 \(F_{浮}\),绿色是 \(F_{弹}\) ,我们发现物体处于平衡状态。所以 \(G = F_{浮} + F_{弹}\)(注:弹力也可能是竖直向下的,但不影响,看成负数即可)。进而我们推出 \(\Delta F_{浮} = \Delta F_{弹}\)。又因为 \(\Delta F_{弹} = k \times \Delta L\),所以 \(k \times \Delta L = \Delta F_{浮} = \rho_{液}gS_{物} \times h_{移}\)。我们设 \(k' = \rho_{液}gS_{物}\),出现我们的第三个式子:
(注:\(k\) 单位是 \(N/cm\),不能取倒数,会出问题)
提示:在多数题目中,\(\rho_{液} = \rho_{水} = 10^3 kg/m^3\),且 \(g\) 取 \(10 N/kg\)。而当 \(S_{物} = 100 cm^2\)时,通过计算发现 \(k' = 1\),因此我们可以直接根据\(k' = \frac{S_{物}}{100cm^2}\)算出。
有了这个比例关系,可以不用方程求解弹簧加水减水问题。
实战
题目: 略。
解答: 略。
FSA第二部分:升降台/物体移动
公式推导
前置:你需要知道相对运动的知识。这样我们就可以将升降台的移动转化为物体自身移动。
先看一张图:
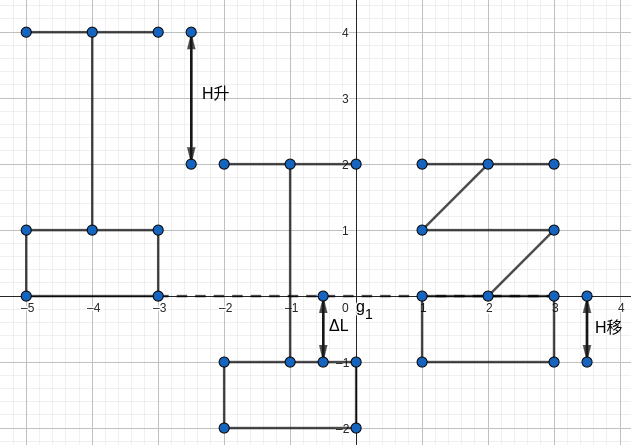
在图中我们把弹簧先看成一根杆,方便理解。然后我们在把他变为弹簧,可以通过位置关系发现第一个式子:
然后同第一部分一样,进行受力分析,得到相同的结论:\(\Delta F_{浮} = \Delta F_{弹} = k \times \Delta L\)。进而得到\(\rho_{液}gS_{物} \Delta h_{浸} = k \times \Delta L\)。
为了推出比例关系,我们必须得到\(\Delta h_{浸}\)与\(h_{移}\)的关系。下面再看一张图:
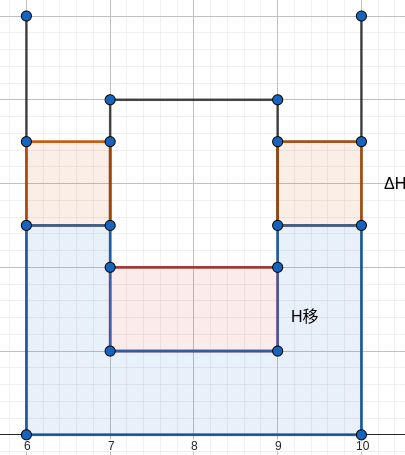
通过这张图可以发现物体在入水后,水会被排开到两边,得到\(\Delta V_{排} = \Delta V_{边}\)以及\(\Delta h_{浸} = h_{移} + \Delta h\)。因此\(\Delta V_{排} = \Delta h_{移} \times S_{物} = \Delta V_{边} = (S_{容} - S_{物}) \times \Delta h\)。最终得出 \(\Delta h = \frac{S_{物}}{S_{容} - S_{物}} \times h_{移}\)。
设\(a = \frac{S_{物}}{S_{容} - S_{物}}\)和\(k' = \rho_{液}gS_{物}\),我们由此得到第二个式子:
实战
题目: 略。
解答: 略。
FSA第三部分:统一理论
其实第一和第二部分都可以统一为一个系统。但用到这个统一系统的题目实在太少(题目没有这么难)。因此我们只给出一张图,读者自行理解不难:
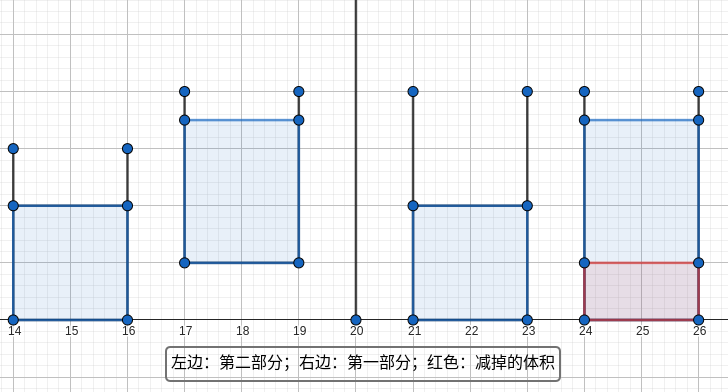
实战
没有题目。