递归电阻
递归电阻是一类神奇的问题。
它可以无限嵌套。
解决它的方法一般是找规律。
实战
已知有如下的电路:
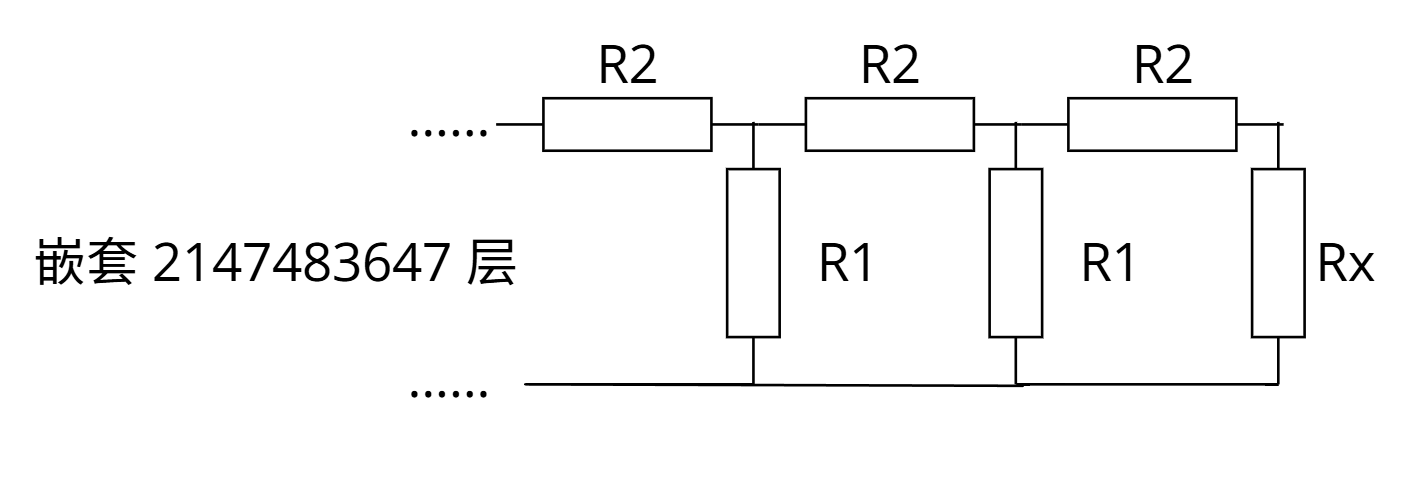
其中 \(R_1=1 \Omega, R_2=2 \Omega, R_x=(1+\sqrt3) \Omega\),求嵌套 \(2147483647\) 层后的等效电阻。
可以先看一层,注意到每一层其实是先把 \(R_2,R_x\) 串联为 \(R_3\),再把 \(R_1\) 和 \(R_3\) 并联。可以计算出每一层的等效电阻为:
\[R = \frac{R_1(R_2+R_x)}{R_1+(R_x+R_2)} = (1+\sqrt3) \Omega\]
我们惊奇地发现,每一层的等效电阻它就等于 \(R_x\)。相当于下一层的 \(R_x\) 就是上一层所有电阻的等效,然后无限递归进行下去。
所以无论嵌套多少层,最后的电阻都是 \((1+\sqrt3) \Omega\)。