不规则电阻
不规则电阻问题是一类神奇的问题(因为可能存在混联)。主要的解决方法是将其等效电路图画出来。
实战
正三角形电阻
如图1-1,现在有一条均匀电阻丝阻值为 \(6R\),用它围一个正三角形 \(ABC\),\(D,E,F\) 分别为三边中点。这 \(6\) 个点每个点都是接线柱,其中 \(D,F\) 用导线连接起来,构成一个不规则电阻。用这个不规则电阻能获得的最大电阻值和最小电阻值(不为 \(0\))分别为多少?
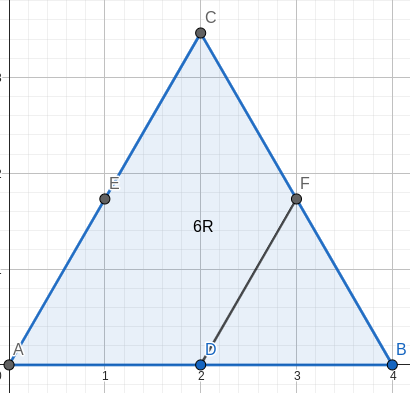
考虑将其转化为等效电路图,用电位差法/节点法将其标出,如图1-2,即可转化。
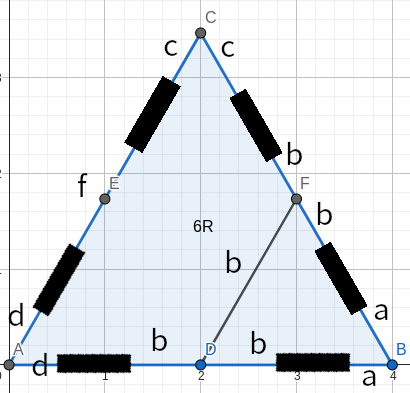
转化后是这样的:
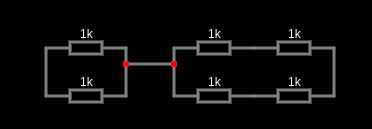
要求最大值,应该是两组并联的串连起来,最大值为 \(1.5R\),最小值应该是并联。
但是究竟是那几个并联呢?我们可以思考以下,电阻都是 \(R\),我们可以让 \(3R\) 与 \(R\) 串联,也可以让 \(2R\) 与 \(2R\) 串联,还可以让 \(R\) 与 \(R\) 串联。经过计算我们发现,第三种情况最小,为 \(0.5R\)。